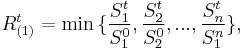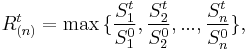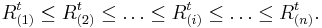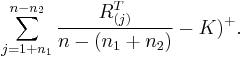Mountain range (options)

Mountain ranges are exotic options originally marketed by Société Générale in 1998. The options combine the characteristics of basket options and range options by basing the value of the option on several underlying assets, and by setting a time frame for the option.

The mountain range options are further subdivided into further types, depending on the specific terms of the options. Examples include:

Everest Options

Although Mount Everest is the highest point on earth, the Everest option payoff is on the worst performer in a basket of 10-25 stocks, with 10-15 year maturity. (Quessette 2002). Given n stocks, 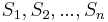S_1, S_2,..., S_n in a basket, the payoff for an Everest option is: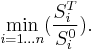 \min_{i=1...n}(\frac{S_i^T}{S_i^0}).

Atlas Options

Atlas was a Titan who supported the Earth on his back. The Atlas option is a call on the mean (or average) of a basket of stocks, with some of the best and worst performers removed. (Quessette 2002). Given n stocks 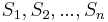S_1, S_2,..., S_n in a basket, define:

R_{(1)}^t=\min{\{\frac{S_1^t}{S_1^0},\frac{S_2^t}{S_2^0},...,\frac{S_n^t}{S_1^n}\}},
R_{(n)}^t=\max{\{\frac{S_1^t}{S_1^0},\frac{S_2^t}{S_2^0},...,\frac{S_n^t}{S_n^0}\}},

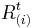where R_{(i)}^t is the i-th smallest return, so that:

R_{(1)}^t \leq R_{(2)}^t \leq \dots \leq R_{(i)}^t \leq \dots \leq R_{(n)}^t.

The Atlas removes a fixed number (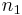n_1) of stocks from the minimum ordering of the basket and a fixed number (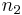n_2) of stocks from the maximum ordering of the basket. In a basket of n stocks, notice that (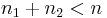n_1%2Bn_2 < n), to leave at least one stock in the basket on which to compute the option payoff. With a strike price K, the payoff for the Atlas option is:

\sum_{j=1%2Bn_1}^{n-n_2}{\frac{R_{(j)}^T}{n-(n_1%2Bn_2)}-K})^{%2B}.
Options
Terms
Swaps
Forwards and Futures
Other derivatives
Market issues